Index columns, selectivity and inequality predicates

So, following on from my post last week, I’m going to take a look at how selectivity and index column order affect inequality predicates.

One thing to note straight off is that the selectivity of a column is much less important for inequality predicates than it was for equality. For equality predicates, the selectivity alone can give a reasonable idea of the number of rows a particular predicate will return. That’s not the case with inequalities. Also, with inequality predicates, the order of columns in the index becomes very important.

One of the most important considerations with inequality predicates is the number of rows that the predicate will return. An identity column may be highly selective, but if the filter is for all rows > 0 and the identity values start t one, then an index on that column is not going to be very useful.

The other consideration when there are inequality predicates is that only that column and columns to the left of it in the index key can be used for index seeks. Any columns to the right of the column with the inequality is no longer eligible for seeking.

To explain with an example, consider our hypothetical table from the previous post (with one small change):

CREATE TABLE ConsideringIndexOrder (
ID INT,
SomeString VARCHAR (100),
SomeDate DATETIME DEFAULT GETDATE()
);  

The same as previously, there’s a single nonclustered index on all three columns, in the order ID, SomeDate, SomeString.

If there’s an inequality predicate, then then the index is only fully seekable for the following queries
…  WHERE ID = @ID AND SomeDate = @dt AND SomeString > @str
…  WHERE ID = @ID AND SomeDate > @dt
…  WHERE ID > @ID

If there’s another predicate, equality or inequality, on a column further to the right in the index, that cannot be executed as part of the index seek, and will be done as a second step, just as happened with equalities when the predicates were not left-based subsets of the index columns.

So, what does that mean for index columns order? Quite simply, if queries are always going to filter with one or more equality predicates and one or more inequality predicates, the columns used for the inequalities must appear further to the right in the index than the equalities.

That’s great when there’s only one inequality predicate, but what happens when there’s more than one? If there are going to be more than one inequality predicate, the one that is likely to return fewer rows should go earlier in the index. This is not to say the most selective one, but the one that will be queried with a more selective range.

Using the above table as an example, if a typical query will run with an inequality on the ID column that on average will return 1000 rows and with an inequality on the date column that will on average return 100 rows, then the date column should go before the ID in the index (assuming that’s the only query)

Let’s take a look at some query scenarios based on the hypothetical table above to see how that index will be used with some inequality predicates.

Scenario 1: Inequality predicate on the ID column

This is probably the simplest of the inequalities. Since ID is the leading column of the index, SQL does a seek to find the beginning of the range (or the first row in the table if applicable) and then reads along the leaf pages of the index until it reaches the end of the range. Those rows are then returned.

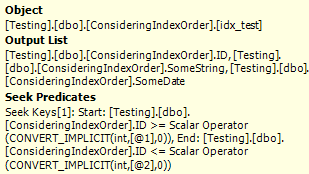
Scenario 2: Equality match on the ID column and inequality on the Date column

This one’s also fairly easy. SQL seeks to find a matching ID and the start of the range and then reads along hte index to find the rest of the rows.

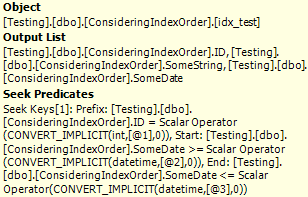
Scenario 3: Inequality match on both the ID and Date columns

In this case, only one of the predicates can be used as a seek predicate, the other will be executed as a predicate, meaning that each row that the seek retrieves has to be compared against that predicate. Since the index starts with ID, it’s the inequality on ID that will be picked for the seek. If there was a second index that started with date, that one might be picked instead.

While both columns are mentioned in the seek predicate, note that there’s also a predicate on the SomeDate column, which is not present in the simple index seeks.