Repairing a replication subscriber
It’s a question which has come up a couple of times. If a subscriber of a transactional replication publication becomes corrupt, is running CheckDB with repair allow data loss safe?
The theory is, since the subscriber is a copy of another database, allowing CheckDB to discard data in the process of repairing won’t actually cause data loss (the data is still there in the publisher).
As with many things, it’s partially true, however there’s a little more to it that just that.
To see why, let’s set up some replication and intentionally corrupt some data in the subscriber and run a repair.
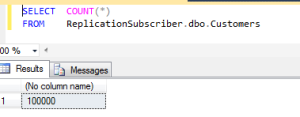
First, the source DB. I’m going to keep it really simple so that we can see the effects. A database with a single table called Customers, populated with 100 000 rows via SQLDataGenerator. The filler column simulates other columns that would be in a real table.
CREATE TABLE Customers ( CustomerID INT IDENTITY PRIMARY KEY, FirstName VARCHAR(50), Surname VARCHAR(50), AccountNumber CHAR(15) UNIQUE, AccountStatus VARCHAR(25), Filler CHAR(200) DEFAULT '' )
Once populated, we set up a transactional replication publication with default settings, and for simplicity have the subscriber be a second database on the same instance. we query the table on the subscriber, we have exactly the same number of rows as the publisher has.
To simulate a misbehaving IO subsystem, I’m going to take the subscription DB offline, open the mdf in a hex editor, scribble on top of a few pages in the user table, then bring the DB back online. A checkDB returns a couple of pages of errors ending with:
CHECKDB found 0 allocation errors and 16 consistency errors in table ‘Customers’ (object ID 421576540).
CHECKDB found 0 allocation errors and 18 consistency errors in database ‘ReplicationSubscriber’.
repair_allow_data_loss is the minimum repair level for the errors found by DBCC CHECKDB (ReplicationSubscriber).
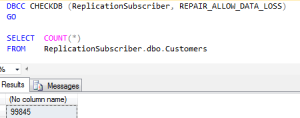
Minimum level to repair is REPAIR_ALLOW_DATA_LOSS and, based on the error messages, doing so will deallocate five pages. Let’s run the repair and then see what’s left in the table.
We’ve lost 155 rows from the Customers table. The replication publisher still has them, but the subscriber now does not. So what happens if someone makes some data modifications on the publisher and changes one of the rows that was lost at the subscriber?
UPDATE dbo.Customers
SET AccountStatus = 'Closed'
WHERE CustomerID = 48700;
GO
INSERT INTO dbo.Customers
(FirstName,
Surname,
AccountNumber,
AccountStatus
)
VALUES ('Mary',
'White',
'4985563214AN'
'Pending'
)
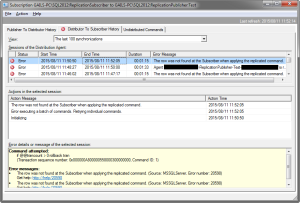
Give it a few seconds to replicate and then let’s check the table in the publisher. The new customer isn’t there… If we go and have a look at the replication, it’s throwing errors.
“The row was not found at the Subscriber when applying the replicated command. “, which is quite true, the row’s not there any longer.
What’s happened is that one of the rows updated on the publisher was lost when CheckDB repaired the database. The rows lost due to the repair weren’t automatically fetched from the publisher, there’s no mechanism in transactional replication for that to happen. Hence when the row was updated on the publisher, the update statement was replicated and the row on the subscriber couldn’t be found, causing the replication to fail, retry and fail again. It will keep failing until it is either reinitialised or the missing row is manually added to the subscriber.
What we needed to have done, to prevent this outcome, was after the CheckDB deallocated pages, to manually (or with something like SQLDataCompare) to sync the subscriber with the publisher and explicitly add back the rows which were on the deallocated pages. The primary key values must be kept the same, as that’s what replication uses to identify which rows in the subscriber need to be updated.
So to go back to the original question, yes it’s probably fine to run CheckDB with repair on a replication subscription, providing that the data deallocated as part of the repair is manually synced from the publisher afterwards. If it isn’t, the replication will break as soon as one of the rows affected by the repair is updated or deleted at the publisher.